第1章 人工智能系统概述

1.2 算法，框架，体系结构与算力的进步

1.2.3 计算机体系结构和计算能力的进步

人工智能芯片通过对深度学习模型中的算子进行抽象，转换为矩阵乘法或非线性变换，根据专用负载特点进一步定制流水线化执行的脉动阵列（Systolic Array），进一步减少访存量（Memory traffic，单位是Bytes），提升计算密度（Arithmetic intensity，单位访存量对应的计算量，单位FLOPs/Byte），提高了性能。

除了算子层面驱动的定制，深度学习本身在算法层常常应用的稀疏性和量化等加速手段也逐渐被硬件厂商根据通用算子定制到专用加速器中（例如，英伟达在 H 系列 GPU 中推出的 Transformer Engine），在专用计算领域进一步引入以往算法框架层才会涉及的优化，进一步优化加速深度学习负载 。

1.2.4 计算框架的进步

深度学习框架对用户提供编程接口，隐藏硬件细节，同时将用户书写的深度学习程序进行编译优化并部署在设备上进行执行。

将框架按照编程范式分类两类：

• 声明式编程（Declarative Programming）
  • 代表性框架：TensorFlow， Keras， CNTK， Caffe2
  • 特点：用户只需要表达模型结构和需要执行的任务，无需关注底层的执行流程，框架提供计算图优化，让用户无需关心底层优化细节，但是对用户来说不容易调试。
• 命令式编程（Imperative Programming）
  • 代表性框架：PyTorch， Chainer， DyNet
  • 特点：用户不仅表达模型结构，还需要表达执行步骤，并且按照每一步定义进行执行，由于无法像声明式编程获取完整计算图并优化后执行，所以难以提供全面的计算图优化，但是由于其简单易用，灵活性高，在模型研究人员中广泛使用。

1.3 深度学习系统组成与生态

1.3.2 深度学习系统的大致组成

过度的抽象会丧失灵活性的表达。

计算图构建：静态，动态计算图构建等。不同的框架类型决定了其使用静态还是动态图进行构建，静态图有利于获取更多信息做全图优化，动态图有利于调试。

编译优化：内核融合等。编译器或框架根据算子的语义，对适合进行内核融合（例如，多个算子和并为一个算子）进行融合，降低内核启动与访存代价。

1.4 深度学习样例背后的系统问题

1.4.2 模型算子实现中的系统问题

我们在深度学习中所描述的层（Layer），一般在深度学习编译器中也称作操作符（Operator）或算子。底层算子的具体实现时先将其映射或转换为对应的矩阵运算（例如，通用矩阵乘 GEMM），再由其对应的矩阵运算翻译为对应的循环程序。

1.4.3 框架执行深度学习模型的生命周期

深度学习框架一般会提供以下功能：

1. 以 Python API 供开发者编写复杂的模型计算图（Computation Graph）结构，调用基本算子实现（例如，卷积的 cuDNN 实现），大幅降低开发代码量。
2. 自动化内存管理，不暴露指针和内存管理给用户。
3. 自动微分（Automatic Differentiation）的功能，并能自动构建反向传播计算图，与前向传播图拼接成统一计算图。
4. 调用或生成运行期优化代码（静态优化）
5. 调度算子在指定设备的执行，并在运行期应用并行算子，提升设备利用率等优化（动态优化）。

PyTorch采用命令式执行（Imperative Execution）方式（运行到算子代码即触发执行，易于调试），TensorFlow 采用符号执行（Symbolic Execution）方式 （程序调用 session.run() 才真正触发执行，并且框架能获取完整计算图进行优化）。

1.5 影响深度学习系统设计的理论，原则与假设

1.5.1 抽象-层次化表示与解释

在冯诺依曼架构（Von Neumann architecture）的 GPU 中分别由指令流水线进行指令存储，加载，解码，并执行指令。通过指令控制，由数据流水线，将数据加载到寄存器，放入 ALU 执行并将结果写回内存。

1.5.3 局部性原则（Priciple of Locality）与内存层次结构（Memory Hierarchy）

GPU 显存和主存（Host memory）之间通过 PCIe 总线传输数据。

1.5.4 线性代数（Linear Algebra）计算与模型缺陷容忍（Defect Tolerance）特性

单指令多线程（SIMT，Single Instruction Multiple Threads）是单指令多数据流（SIMD，Single Instruction Multiple Data）的执行方式，SIMT同时提供 CUDA 并行编程模型和 FMA 等向量化 PTX 指令。这种方式很适合矩阵计算，因为其控制流少，一批线程（在 NVIDIA GPU 中称作束（Warp），一般为 32 个线程为一个束统一调度，执行相同指令处理不同数据）可以在很长时间内执行相同指令，所以对适合编译和转换为矩阵计算的上层应用（深度学习，图像处理等），非常适合采用 GPU 进行加速。

第3章 深度学习框架基础

3.1 基于数据流图的深度学习框架

3.1.1 深度学习框架发展概述

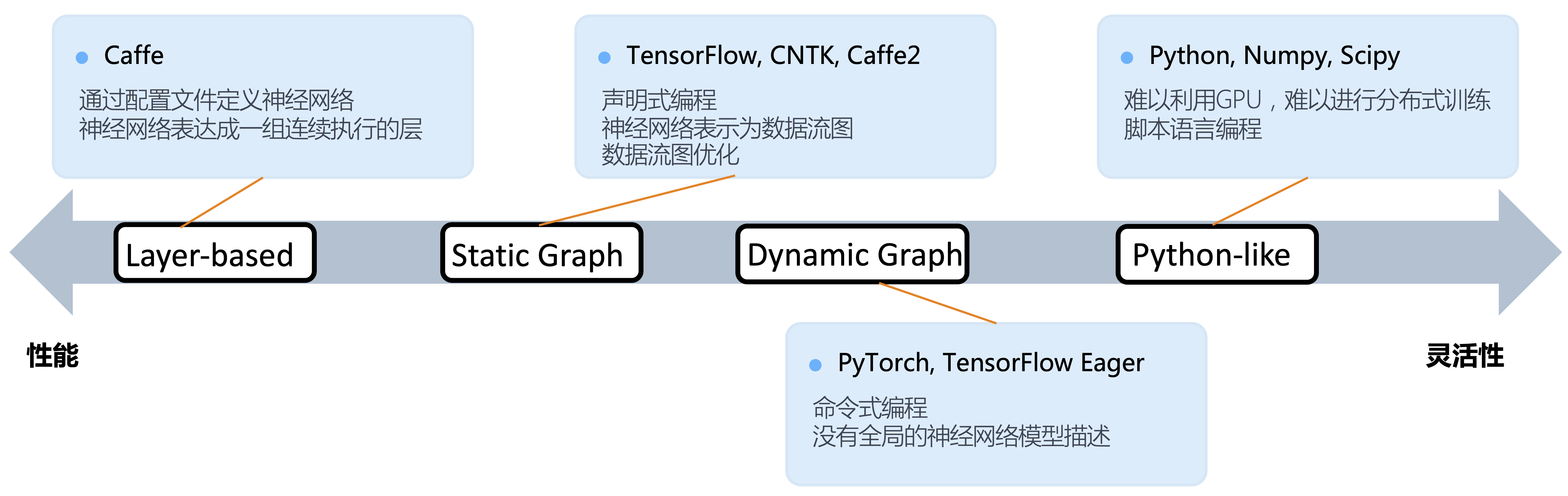
到目前阶段，神经网络模型结构越发多变，涌现出了大量如：TensorFlow Eager，TensorFlow Auto-graph，PyTorch JIT，JAX这类呈现出设计选择融合的深度学习框架设计。这些项目纷纷采用设计特定领域语言(Domain-Specific Language，DSL）的思路，在提高描述神经网络算法表达能力和编程灵活性的同时，通过编译期优化技术来改善运行时性能。

3.1.2 编程范式：声明式和命令式

深度学习框架为前端用户提供声明式（Declarative Programming）和命令式（Imperative Programming）两种编程范式来定义神经网络计算。

• 声明式编程（Declarative Programming）
  • 前端语言中的表达式不直接执行，而是首先构建起一个完整前向计算过程表示，这个计算过程的表示经过序列化发送给后端系统，后端对计算过程表示优化后再执行，又被称作先定义后执行（Define-and-Run）或是静态图。
  • 代表性框架：TensorFlow， Keras， CNTK， Caffe2
  • 优点：对数据和控制流的静态性限制更强，由于能够在执行之前得到全程序描述，从而有机会进行运行前编译（Ahead-Of-Time）优化。
  • 缺点：不易调试。
• 命令式编程（Imperative Programming）
  • 后端高性能可复用模块以跨语言绑定（Language Binding）方式与前端深度集成，前端语言直接驱动后端算子执行，用户表达式会立即被求值，又被称作边执行边定义(Define-by-Run)或者动态图。
  • 代表性框架：PyTorch， Chainer， DyNet
  • 优点：方便调试，灵活性高。
  • 缺点：由于在执行前缺少对算法的统一描述，失去了编译期优化（例如，对数据流图进行全局优化等）的机会。

两种编程范式之间并不存在绝对的边界，多阶段（Multi-Stage ）编程和即时编译（Just-In-Time, JIT）技术能够实现两种编程模式的混合。随着TensorFlow Eager和PyTorch JIT的加入，主流深度学习框架都选择了通过支持混合式编程以兼顾两者的优点。

3.1.3 数据流图

在运行神经网络计算之前，编译期分析能够对整个计算过程尽可能进行推断，为用户程序补全反向计算，规划执行，从而最大程度地降低运行时开销。

数据流图（Dataflow Graph）是一种描述计算的经典方式，广泛用于科学计算系统。为了避免在调度执行数据流图时陷入循环依赖，数据流图通常是一个有向无环图。在深度学习框架中，图中的结点是深度学习框架后端所支持的操作原语（Primitive Operation），不带状态，没有副作用，结点的行为完全由输入输出决定；结点之间的边显式地表示了操作原语之间的数据依赖关系。图3中的圆形是数据流图中边上流动的数据，方形（节点）是数据流图中的基本操作。

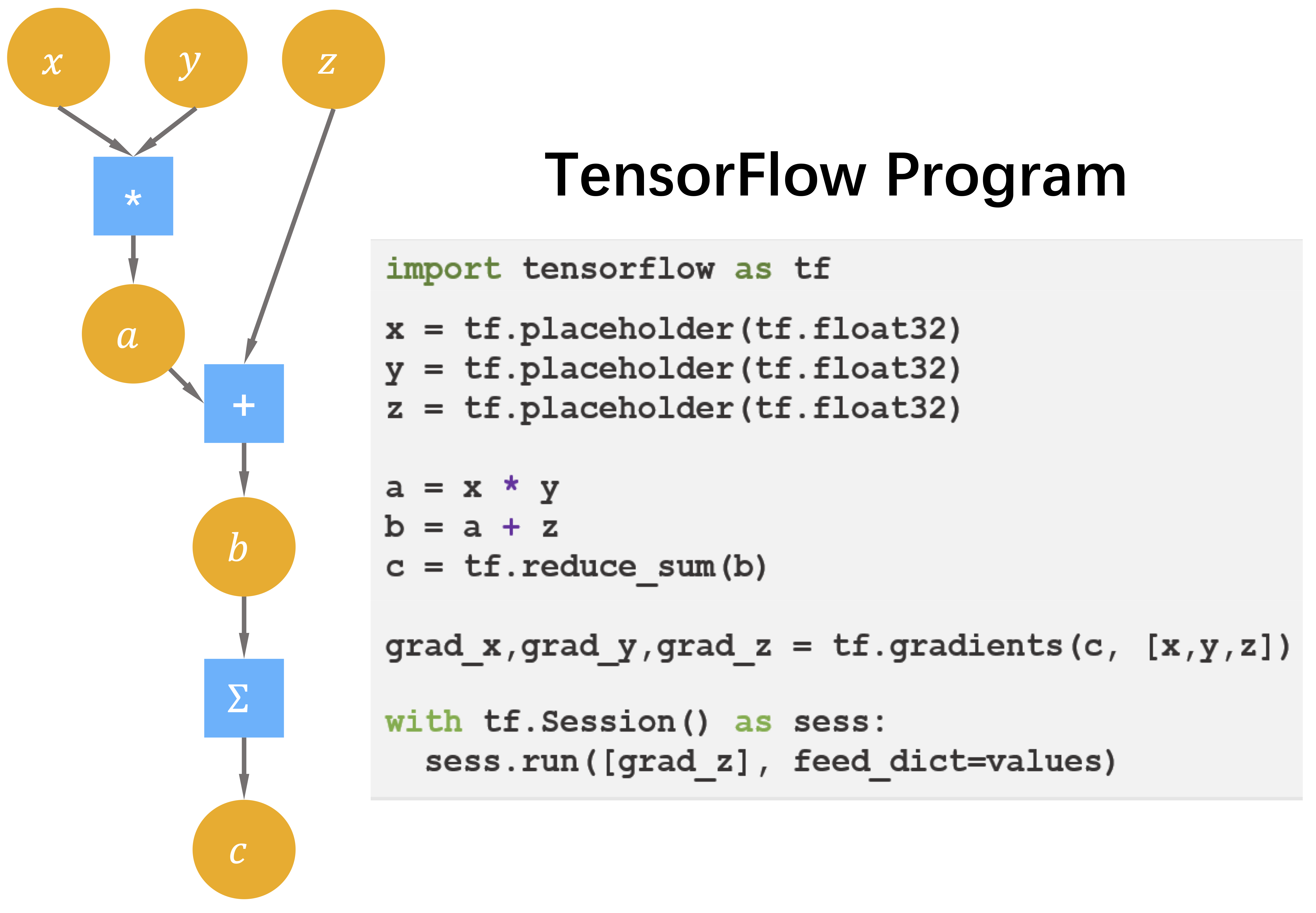
张量计算非常适合在单指令多数据（SIMD，Single Instruction, Multiple Data）加速器上进行加速实现。

主流深度学习框架将神经网络计算抽象为一个数据流图（Dataflow Graph），也叫做计算图，图中的节点是后端支持的张量操作原语，节点之间的边上流动着张量。一类最为重要的操作是张量上的数值计算，往往有着极高的数据并行度，能够被硬件加速器加速。

自动微分（Automatic Differentiation，简称Auto-diff）系统要解决的问题是给定一个由原子操作构成的复杂计算程序，如何为其自动生成梯度计算程序。自动微分是深度学习框架的核心组件之一。

自动微分按照工作模式可分为：

• 前向自动微分：深度学习系统很少采用。时间复杂度为$O(n)$，$n$是输入变量的个数$n$。无需存储中间层前向计算结果。

• 反向自动微分：时间复杂度为$O(m)$，$m$是输出变量的个数。需存储中间层前向计算结果，使用类似于先进后出的栈，越接近输入的前向计算结果越晚被用于反向微分时计算梯度，所以网络越深，反向微分会消耗越多的内存。

对前向和反向这两种自动微分模式：

1. 由于在神经网络训练中，总是输出一个标量形式的网络损失，于是$m=1$，反向微分更加适合神经网络的训练。
2. 当$n=m$时，前向微分和反向微分没有时间复杂度上的差异。但在前向微分中，由于导数能够与前向计算混合在一轮计算中完成，因此不需要存储中间层前向计算结果，落实到更具体的高效实现中，也会带来更好的访问存储设备的局部性，因此前向微分更有优势。
3. 通常神经网络的整体训练采用反向微分的计算复杂度更低，但在局部网络使用前向微分依然是可能的。

自动微分按照实现方式可为：

• 基于对偶数（Dual Number）的前向微分：常实现于程序语言级别的自动微分系统中。
• 基于磁带（Tape）的反向微分：常实现于以PyTorch为代表的边定义边执行类型的动态图深度学习系统中。
• 基于源代码变换的反向微分：常实现于以TensorFlow为代表先定义后执行类型的静态图深度学习系统中。

3.2 神经网络计算中的控制流

3.2.1 背景

RNN和Attention机制的计算过程依赖于循环控制，为了支持有控制流结构的神经网络计算，主流深度学习框架采用了两类设计思路：

• 后端对控制流语言结构进行原生支持，计算图中允许数据流和控制流的混合，例如Tensorflow采用这种思路。
• 复用前端语言的控制流语言结构，用前端语言中的控制逻辑驱动后端数据流图的执行，例如Pytorch采用这种思路。

3.2.2 静态图：向数据流图中添加控制流原语

TensorFlow中控制流方案的概况，整体分为：暴露给前端用户用于构建计算图的前端API，这些API会被转换成更低等级的控制流原语：Enter，Switch，Exit，Merge，NextIteration，使用这些原语对计算图进行扩展，再由计算图优化器进一步进行改写。

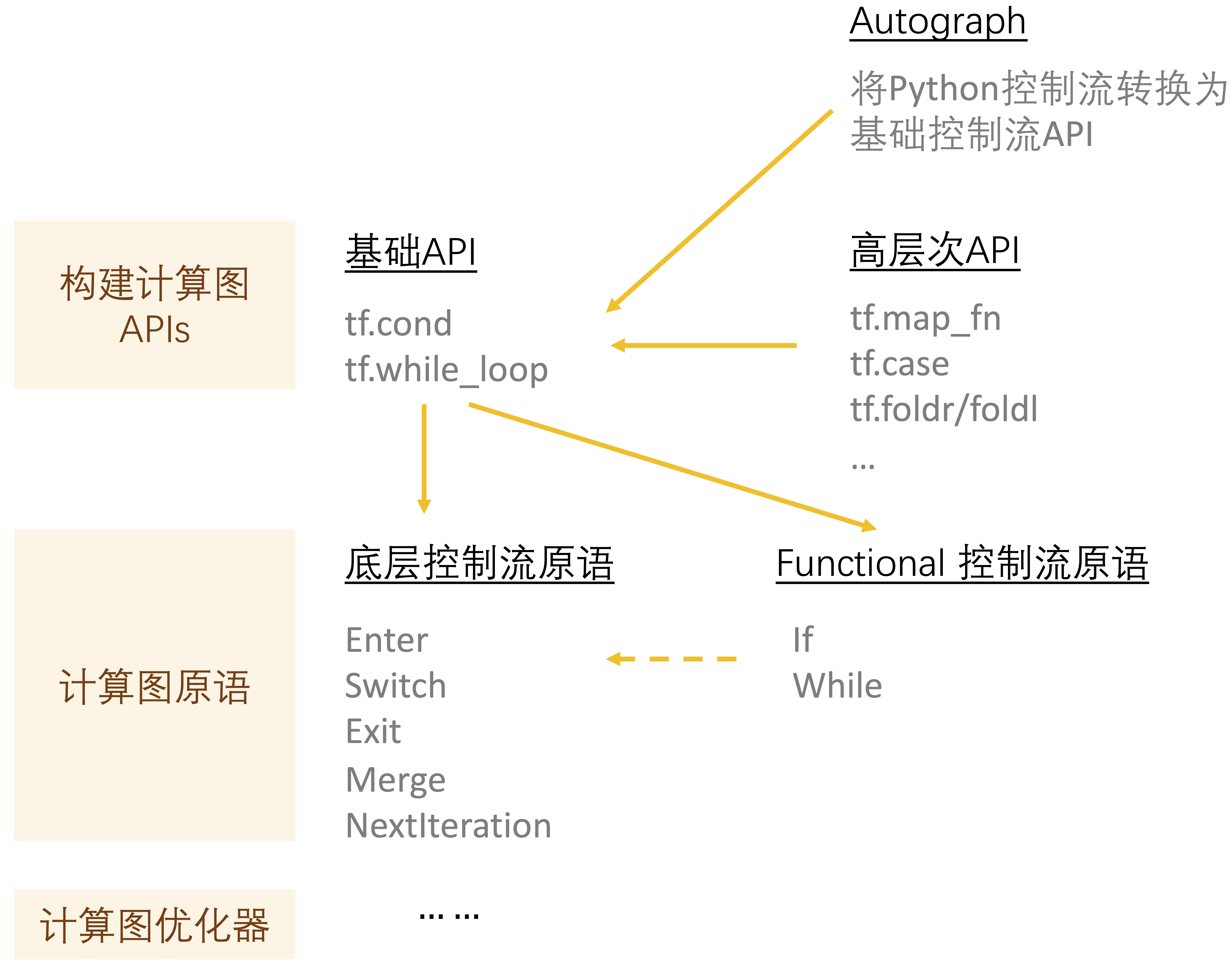
3.2.3 动态图：复用宿主语言控制流语句

Pytorch使用Python作为宿主语言。与静态图不同，这时框架不再维护一个全局的神经网络算法描述，神经网络变成一段Python代码，后端的张量计算以库的形式提供，维持了与numpy一致的编程接口。

该方式灵活性高、便于用户调试，为用户带来一种使用体验上的错觉：定义神经网络计算就像是编写真正的程序，但缺点也是明显的：用户容易滥用前端语言特性，带来更复杂且难以优化性能问题。并且，在这种设计选择之下，一部分控制流和数据流被严格地隔离在前端语言和后端语言之中，跨语言边界的优化十分困难，执行流会在语言边界来回跳转，带来十分严重的运行时开销。

3.2.4 动态图转换为静态图

静态图易于优化但灵活性低，动态图灵活性高但由于缺少统一的计算过程表示难以在编译期进行优化。

以TensorFlow的Auto-graph和PyTorch的JIT为代表，主流深度学习框架最终都走向了探索动态图与静态图的融合：限制能够使用的前端宿主语言语法要素，前端用户使用宿主语言中的控制流语句编写神经网络程序，调试完毕后，通过语法分析器（Parser）自动解析出对后端优化更加友好的静态子图。但这并不能完全解决控制流的优化难题。

动态图向静态图转换分为基于追踪（Tracing）和基于源代码解析（Parsing）两种方式。

第4章 矩阵运算与计算机体系结构

4.2 计算机体系结构与矩阵运算

4.2.1 CPU体系结构

CPU体系结构并不是针对计算密集型任务而设计的，其主要支持的计算是如何高效地执行通用程序，为了能够灵活地支持不用类型的计算任务，一个CPU核上需要引入较为复杂的控制单元来优化针对动态程序的调度，由于一般的计算程序的计算密度低，因此，CPU核上只有较少量的算术逻辑单元（ALU）来处理数值类型的计算。在CPU核上执行一条计算执行需要经过一个完整的执行流水线，包括读取指令、译码、在ALU上计算结果、和写回，在整个流水线上，大量的时间和功耗都花在了ALU之外的非计算逻辑上。

4.3 GPU体系结构与矩阵运算

4.3.1 GPU体系结构

与CPU相比，GPU的体系架构中的一个最大特点就是增加了大量的运算单元ALU，如图4.3.1所示。通常GPU的一个处理器（也叫做流式多处理器，Streaming Multiprocessor）包括数十甚至上百个简单的计算核，整个GPU可以达到上千个核。与CPU相比，每个核的结构简单了很多，通常不支持一些CPU中使用的较为复杂的调度机制。

在执行指令的时候，为了充分利用每一次读取指令带来的开销，GPU会以一组线程为单位同时执行相同的指令，即SIMT（单指令多线程）的方式，如图4-3-1右半部分所示。在CUDA GPU上，一组线程称为warp，一个warp有32个线程，每个线程执行相同的指令但访问不同的数据。

4.3.2 GPU编程模型

为了将一个并行程序映射到GPU的多级并行度上，CUDA中首先将一组线程（通常不超1024个）组成一个线程块（block），每个线程块中的线程又可以分成多个warp被调度到GPU核上执行，一个线程块可以在一个SM上运行。多个线程块又可以组成一个网格（grid）。

4.3.3 GPU实现一个简单的计算

和CPU不一样的是，GPU上每个SM通常有一块共享内存（Shared memory）可供所有线程共享访问和存储数据，其访问延时基本和L1缓存接近。

第5章 深度学习的编译与优化

深度学习的编译与优化就是将当前的深度学习计算任务通过一层或多层中间表达进行翻译和优化，最终转化成目标硬件上的可执行代码的过程。

5.1 深度神经网络编译器

编译器（compiler）在计算机语言编译中往往指一种计算机程序，它会将某种编程语言写成的源代码（原始语言）转换成另一种编程语言（目标语言），在转换的过程中进行的程序优化就是编译优化过程。与传统程序语言编译器类似，深度神经网络编译器的提出主要也是解决多种设备适配性和性能优化的问题，也分为前端（Frontend）、后端（Backend）、中间表达（Intermediate Representation, IR）和优化过程（Optimizaiton Pass）等。

5.1.2 后端

不同的类型的计算设备往往采用完全不同的芯片架构，从而对应的编程模型和优化也完全不同。如CUDA GPU采用的是多个并行的流式处理器（Streaming Multiprocessor）和共享内存的架构，在GPU上执行的代码需要符合SIMT（Single Instruction Multiple Threads）的计算模型；而CPU一般采用的是多核架构，以及多线程模型（如线程池）来实现高性能的计算任务。

5.1.3 中间表达

每个DNN编译器也会定义自己的计算图格式，一般这些计算图都可以进行等价互相转换。

5.1.4 优化过程

深度神经网络编译器的优化过程（Optimization Pass）的输入是某一种中间表达，经过一系统优化和变化过程，输出一个新的被优化过后的中间表达。后续重点介绍四个类型的优化过程，分别是：计算图优化、内存优化、内核优化和调度优化。

5.2 计算图优化

计算图是一个有向无环图（DAG），节点表示算子，边表示张量或者控制边（control flow）。

计算图优化方法：算术表达式化简，公共子表达式消除，常数传播，矩阵乘自动融合，算子融合，子图替换和随机子图替换，等等。

5.3 内存优化

这章节介绍的都是无损内存优化方法：基于拓扑序的最小内存分配，张量换入换出，张量重计算，等等。

有些场景，无损内存优化方法都不足以达到目标时，也会采取一些有损的内存优化，如量化、有损压缩等等。

5.4 内核优化与生成

前面的编译优化基本都是在计算图的上进行的，当一个计算图被优化过后，就需要继续向下编译，最主要的是对计算图中的每一个算子生成相应的代码。

5.5 跨算子的全局调度优化

第6章 分布式训练算法与系统

6.1 分布式深度学习计算简介

6.1.3 深度学习的并行化训练

将深度学习训练的并行化基本方案划分为算子内并行和算子间并行。

算子内并行保持已有的算子的组织方式，探索将单个深度学习算子有效地映射到并行硬件设备上的执行。算子内并行主要利用线性计算和卷积等操作内部的并行性。通常一个算子包含多个并行维度，常见的例如：批次（Batch）维度（不同的输入样本（Sample））、空间维度（图像的空间划分）、时间维度（RNN网络的时序展开）。在目前主流的深度学习框架中，这些并行的维度通过SIMD架构等多执行单元达到同时并行运算的目的。

算子间并行则更注重发掘多个算子在多个设备上并行执行的策略，甚至解耦已有的单个算子为多个等效算子的组合，进一步发掘并行性。算子间并行的形式主要包括：数据并行（多个样本并行执行）；模型并行（多个算子并行执行）；组合并行（多种并行方案组合叠加）。

6.2 分布式训练算法分类

6.2.1 数据并行

每个设备分别拥有完整的模型副本。不适合模型参数量超过单设备内存的场景。

数据并行的步骤如下：

1. 不同设备上读取不同数据
2. 执行相同计算图
3. 跨设备AllReduce聚合梯度
4. 利用聚合后梯度更新模型

需要注意的是，有些模型的操作，例如批归一化(BatchNorm)，理论上需要额外的处理才能保持并行化的训练数学性质完全不变。

6.2.2 模型并行

模型并行(Model-Parallelism)将模型参数进行划分并分配到多个设备上。根据划分模型参数的方式不同，模型并行的常见的形式包含张量并行和流水并行。

张量并行是通过拆分算子，并把拆分出的多个算子分配到不同设备上并行执行。

流水线并行依照模型的运算符的操作将模型的上下游算子分配为不同的流水阶段（Pipeline Stage），每个设备负责其中的一个阶段模型的存储和计算。改进的流水线并行包括GPipe、PipeDream等。

6.2.4 并行方式的对比分析

	非并行	数据并行	模型并行
设备输入数据量	1	1/N	1
传输数据量	0	模型/梯度大小	激活大小
总存储占用	1	~N	1
负载平衡度	-	强	弱
并行限制	-	单步样本量	算子数量

表6-3-1: 不同并行方式的比较 (设备数量：N)

相较而言，数据并行会增加模型的存储开销，而模型张量并行会增加数据的重复读取。

在实际中，更普遍的做法是同时结合多种并行方式来进行整个模型训练的并行划分。例如FlexFlow、tofu、GSPMD采用了数据和张量并行，PipeDream 同时采用了数据并行和流水并行，Megatron-LM针对于包含BERT、GPT的Transformer模型家族同时启用了数据并行、张量并行和流水并行，综合发挥各个方式的优势。

6.3 深度学习并行训练同步方式

在多设备进行并行训练时，可以采用不同的一致性方式，对应其间不同的通信协调方式，大致可分为：同步并行、异步并行、半同步并行。

6.3.1 同步并行

同步并行是采用具有同步障的通信协调并行。阻止所有工作节点在全部通信完成之前继续下一轮计算是同步障。

6.3.2 异步并行

采用不含同步障的通信协调并行。

6.3.2 半同步并行

采用具有限定的宽松同步障的通信协调并行。

6.4 分布式训练系统简介

分布式训练系统通常分为：分布式用户接口、单节点训练执行模块、通信协调三个组成部分。

图6-4-3: 采用参数服务器并行的数据流图

6.4.2 PyTorch 中的分布式支持

与TensorFlow相对的，PyTorch 的用户接口更倾向于暴露底层的通信原语用于搭建更为灵活的并行方式，这样的设计思想并不包含TensorFlow中系统下层的数据流图抽象上的各种操作，而将整个过程在用户可见的层级加以实现，相比之下更为灵活，但在深度优化上欠缺全局信息。

PyTorch的通信原语包含点对点通信和集体式通信。集体式通信包含了一对多的 Scatter / Broadcast， 多对一的 Gather / Reduce 以及多对多的 All-Reduce / AllGather。

6.4.3 通用的数据并行系统Horovod

Horovod专注于数据并行的优化，并广泛支持多种深度学习框架的分布式训练，且强调易用性。

6.5 分布式训练的通信协调

分布式训练的通信，按照方式可分为

• 机器内通信，包括：共享内存、GPU Direct P2P over PCIe、GPU Direct P2P over NVLink。
• 机器间通信，包括：TCP/IP网络、 RDMA网络和GPU Direct RDMA网络。

6.5.1 通信协调的硬件

NVLink (300GB/s) vs. PCIe 4.0 (32GB/s)

6.5.2 通信协调的软件

NVIDIA提出了针对其GPU等硬件产品的通信库 NCCL: NVIDIA Collective Communication Library。NCCL提供类似MPI的通信接口，包含集合式通信（collective communication）all-gather、 all-reduce、 broadcast、 reduce、reduce-scatter 以及点对点(point-to-point)通信send 和receive。

第8章 深度学习推理系统

8.1 推理系统简介

推理系统中的性能优化的策略分为在线和离线策略。

离线策略是在模型还没有加载到推理系统内存部署的阶段，对模型本身进行的转换，优化与打包，核心是让模型变得更“小”（运算量小，内存消耗小等），进而精简模型，更像传统编译器所解决的静态分析与优化的问题。

在线部分是推理系统加载模型后，运行时对请求和模型的执行进行的管理和优化。其更多与运行时资源分配与回收，任务调度，扩容与恢复，模型管理协议等相关，更像传统操作系统与 Web 服务系统中所解决的运行时动态管理与优化的问题。

图 8.1.9 推理系统中涉及到的策略与优化

8.2 模型推理的离线优化

本章节的优化都在朝着下面的思路设计：

（1）更小的模型：更小的模型意味着更少的浮点运算量和访存开销。例如，低精度推理，模型压缩等。 （2）更小的访存开销：层间与张量融合，目标后端自动调优等。 （3）更大的并行度：目标后端自动调优等。 同时本章的优化属于 离线优化 ，也就是属于部署推理模型之前做的优化，对这段优化处理本身的开销没有严格约束。

8.2.2 推理（Inference）延迟（Latency）

推理系统常常可以通过以下几个方向进行模型推理的延迟优化：

• 模型优化，降低访存开销：
  • 层（Layer）间融合（Fusion）或张量（Tensor）融合
  • 目标后端自动调优
  • 内存分配策略调优
• 降低一定的准确度，进而降低计算量，最终降低延迟：
  • 低精度推理与精度校准（Precision Calibration）
  • 模型压缩（Model Compression）
• 自适应批尺寸（Batch Size）：动态调整需要进行推理的输入数据数量
• 缓存（Caching）结果：复用已推理的结果或特征数据

8.2.3 层（Layer）间与张量（Tensor）融合

我们将模型抽象为数据流图（Data-Flow Graph)，其中在设备执行的层（Layer）在一些框架内也称作内核（Kernel）或算子（Operator）。设备中执行一个内核，一般需要以下几个步骤和时间开销，启动内核，读取数据到设备，执行内核，结果数据写回主存。将内核融合问题抽象为一个优化问题：搜索计算图的最优融合策略，降低内核启动，数据访存读写和内存分配与释放开销。

图 8.2.3 使用内核融合进行模型执行优化

8.2.4 目标后端自动调优

程序分析（Program Analysis）与编译器（Compiler）领域在过去的几十年中，对循环做了大量的研究与优化，例如：循环分块（Tiling），循环展开（Unrolling），循环交换（Interchange），循环分解（Fission），循环融合（Fusion）等。而面对如此大的优化空间，当前的工作更多的是通过更高效的算法搜索或通过机器学习的方法，近似或超过专家手工优化的效果，以及通过编译器工程上适配更多类型设备。

8.2.5 模型压缩

常用的模型压缩技术有：

• 参数裁剪（Parameter Pruning）和共享（Sharing）
  • 剪枝（Pruning）
  • 量化（Quantization）
  • 编码（Encoding）
• 低秩分解（Low-Rank Factorization）
• 知识精炼（Knowledge Distillation）
• …

例如，在 Deep Compression ICLR ‘16的工作中，将模型压缩抽象为以下几个步骤：

1. 剪枝阶段：此阶段可以减少权重近10倍。需要再微调训练以还原预测精度。
2. 量化阶段：此阶段可压缩27到31倍。网络量化和权重共享进一步压缩减少网络权重比特。网络量化中会对权重进行聚类，生成并利用统计出的代码书（Code Book）进一步量化权重。权重共享对输入数据通过一个哈希函数决定选择哪些权重。此步骤需要再微调训练以还原预测精度。
3. 霍夫曼编码（Huffman Encoding）阶段：此阶段可提升压缩35到49倍。霍夫曼编码是一种优化的前缀编码，通常用于数据压缩。

8.2.6 低精度推理

由于不需要进行反向传播求梯度，因此相比训练常常使用的 FP32，推理可以使用半精度 FP16 甚至 INT8 张量运算降低计算量和内存占用。

8.3 部署

8.3.3 模型转换与开放协议

ONNX 是一种用于表示机器学习模型的开放转换格式。ONNX 定义了一组通用运算符（机器学习和深度学习模型的构建块），以及一种通用文件格式。ONNX 标准成为衔接不同框架与部署环境（服务端和移动端）的桥梁。

在模型转换工具MMdnn中，模型可以通过模型框架的模型解析器（Parser）、中间表达（IR）、目标模型框架的模型发射器（Emitter）实现跨框架转换。

8.4 推理系统的运行期优化

8.4.1 推理系统的吞吐量

推理系统达到高吞吐的常见优化策略有：

• 利用加速器并行
  • 批处理请求（Request）
  • 利用优化的 BLAS 矩阵运算库，SIMD 指令和 GPU 等加速器加速，提升利用率
• 自适应批尺寸（Batch Size）
• 多模型装箱使用加速器
• 扩展到多模型副本（Replica）部署

8.6 推理专有芯片

8.6.1 推理芯片架构对比

深度学习模型部署：

• CPU 部署：硬件层面减少跨 PCIe 搬运到 GPU 的开销。
• GPU 部署：NVIDIA 的 GPU 采用 SIMT 的架构，其抽象调度单位为束（Warp），也就是一组线程按 SIMD 模型执行，进一步精简指令流水线让出更多芯片面积放入计算核，同时减少指令访存。
• ASIC 部署：相比 GPU，ASIC 一般可以根据负载特点设计脉动阵列（Systolic Array）架构，其根据负载的数据流特点设计计算器件的排布，让计算单元输入与输出流水线化，减少访存。除了上面提到的基本脉动阵列，一般我们可以将深度学习模型中抽象出两类算子：（1）通用矩阵乘：例如，卷积，全连接，RNN 等算子。（2）非线性计算：例如，激活函数，平均池化等。对应两大类算子，一般的神经网络芯片中会设计对应的专用计算单元。

• FPGA 部署：相比 ASIC 和 GPU，通过 FPGA 部署也像一种专用芯片部署的动机一样，以期获取更好的性能能耗比。但是相比 ASIC 两者主要区别，一般可以通过规模去区分和考虑，在一定规模下 FPGA 更加节省成本，而超过一定规模 ASIC 成本更低。

8.6.2 神经网络推理芯片的动机和由来

TPU 的推理芯片去掉了以下功能：缓存（Caches）， 分支预测（Branch Prediction）， 乱序执行（Out-of-order Execution），多道处理（Multiprocessing），推测预取（Speculative Prefetching），地址合并（Address Coalescing），多线程（Multithreading），上下文切换（Context Switching）。从而节省空间排布更多的计算器件。

第11章 模型压缩与加速

11 前言

模型压缩方法主要包括：数值量化（Data Quantization），模型稀疏化（Model sparsification），知识蒸馏（Knowledge Distillation）， 轻量化网络设计（Lightweight Network Design）和张量分解（Tensor Decomposition）。 本章第1节将首先对这些压缩技术进行简要介绍。 其中模型稀疏化是应用最为广泛的一种模型压缩方法，可以直接减少模型中的参数量。本章第2节将对基于稀疏化的模型压缩方法进行详细介绍。经过压缩后的模型并一定适用于原有通用处理器，往往需要特定的加速库或者加速硬件的支持。本章第3节将介绍不同模型压缩算法所适应的硬件加速方案。

11.1 模型压缩简介

11.1.2 模型压缩方法

数值量化

量化在数字信号处理领域是指将信号的连续取值近似为有限多个离散值的过程，可以认为是一种信息压缩的方法。 而在深度学习中，数值量化是一种非常直接的模型压缩方法，例如将浮点数（Floating-point）转换为定点数（Fixed-point）或者整型数（Integer），或者直接减少表示数值的比特数（例如将 FP32 转换为 FP16 ，进一步转化为 Int16 ，甚至是 Int8 ）。更低的比特位宽通常意味着更快的访存速度和计算速度，以及更低的功耗。

表11.1.1 常用的模型训练数制选项

Number format	Full name	Total bits	Sign	Exponent	Fraction
FP32	Floating-point 32	32	1	8	23
TF32	TensorFloat-32	19	1	8	10
FP16	Floating-point 16	16	1	5	10
BP16	Brain floating-point 16	16	1	8	7

数值量化方法根据量化对象可以分为：

• 权值量化
• 激活量化

模型训练由于需要反向传播和梯度下降，对数值精度要求更高，FP16、TF32、BF16等浮点格式更适合。

模型稀疏化

稀疏化方法直接“删除”部分模型参数。深度神经网络中存在很多数值为零或者数值接近零的权值，合理的去除这些“贡献”很小的权值，再经过对剩余权值的重训练微调，模型可以保持相近甚至相同的准确率。

稀疏化方法根据稀疏化的对象可以分为：

• 权值剪枝：减少神经网络中的连接数量
• 神经元剪枝：减少神经网络中的节点数量

当然神经元剪枝后也会将相应的连接剪枝，当某个神经元的所有连接被剪枝后也就相当于神经元剪枝。

对于很多神经网络来说，剪枝能够将模型大小压缩 10 倍以上，这就意味着可以减少10倍以上的模型计算量，结合定制硬件的计算力提升，最终可能达到更高的性能提升。

权值剪枝是应用最为广泛的模型稀疏化方法。权值剪枝通常需要寻找一种有效的评判手段，来评判权值的重要性（例如权值的绝对值大小），根据重要性将部分权值（小于某一个预先设定好的阈值）剪枝掉。

权值剪枝的缺点是不同模型的冗余性不同，过度剪枝后模型的准确率可能会有所下降，需要通过对模型进行重训练，微调剩余权值以恢复模型的准确率。甚至需要多次迭代剪枝和微调的过程以达到最好的压缩率和模型精度。

这种针对每一个权值的细粒度剪枝方法使得权值矩阵变成了没有任何结构化限制的稀疏矩阵，引入了不规则的计算和访存模式，对高并行硬件并不友好。后续的研究工作通过增加剪枝的粒度使得权值矩阵具有一定的结构性，更加有利于硬件加速。粗粒度剪枝方法以一组权值为剪枝对象，例如用一组权值的平均值或最大值来代表整个组的重要性，其余的剪枝和重训练方法与细粒度剪枝基本相同。例如，文献以二维矩阵块为剪枝粒度，这种方法通常被成为块稀疏（Block Sparsity）。在CNN中对Channel、Filter 或 Kernel进行剪枝，同样增加了剪枝粒度，也可以认为是粗粒度剪枝。

基于剪枝的稀疏化方法是一种启发式的搜索过程，缺乏对模型准确率的保证，经常面临模型准确率下降，尤其是在粗粒度剪枝中或追求高稀疏度中。为了解决这个问题，研究人员将模型稀疏化定义为一个优化问题，利用AutoML等自动化方法寻找最佳的剪枝位置和比例等。第 11.2 节将对基于稀疏化的模型压缩方法进行详细介绍。

知识蒸馏

知识蒸馏是一种基于教师-学生网络的迁移学习方法。 为了压缩模型大小，知识蒸馏希望将一个大模型的知识和能力迁移到一个小模型中，而不显著的影响模型准确率。 知识蒸馏由三个关键部分组成：知识，蒸馏算法和教师-学生网络架构，研究人员针对不同的任务提出了许多蒸馏算法和教师-学生网络架构。 近年来，知识蒸馏方法已扩展到师生学习，相互学习，终身学习和自身学习等。

轻量化网络设计

神经网络架构搜索（Neural Architecture Search, NAS）。

张量分解

张量（矩阵）计算是深度神经网络的基本计算单元，直接对权值张量进行压缩可以实现模型的压缩与加速。 基于张量分解的压缩方法主要是将一个庞大的参数张量分解成多个更小的张量相乘的方式。 例如将一个二维权值矩阵进行低秩分解，分解成两个更小的矩阵相乘。主要的张量分解方法包括 SVD 分解，Tucker 分解和 CP 分解等。张量分解的实现涉及计算成本高昂的分解操作。对权值张量分解后可能会对原有模型准确率造成影响，需要大量的重新训练来达到再次收敛。

小结与讨论

在实际应用中，不同的压缩方法往往可以组合使用以达到更高的压缩率，例如对轻量化网络进行稀疏化或数值量化。组合使用多种压缩方法虽然可以达到极致的压缩效果，但增加了多种模型配置超参数，结合NAS和AutoML等方法可以减轻搜索压缩方法的负担。

11.2 基于稀疏化的模型压缩

11.2.1 人类大脑的稀疏性

生物研究发现人脑是高度稀疏的。

11.2.2 深度神经网络的稀疏性

根据神经网络中可以被稀疏化的对象，稀疏性主要包括权重稀疏、激活稀疏和梯度稀疏。

权重稀疏

许多层权重的数值分布很像是正态分布（或者是多正态分布的混合），越接近于0，权重就越多。舍弃掉其中接近0值的权重，相当于在网络中剪除部分连接，对网络精度影响不大，这就是权重剪枝。

即使是移除绝对值接近于0的权重也会带来推理精度的损失。为了恢复网络精度，通常在剪枝之后需要进行再次的训练，这个过程称为微调（fine-tuning）。微调之后的权重分布将部分地恢复高斯分布的特性，同时网络精度也会达到或接近剪枝前的水平。大多数的权重剪枝算法都遵循这一“正则化-剪枝-微调”反复迭代的流程。

激活稀疏

神经网络模型中的非线性激活单元（activation）是对人类神经元细胞中轴突末梢（输出）的一种功能模拟。

ReLU激活函数输出结果中存在高度的稀疏性。

梯度稀疏

在神经网络模型训练早期，各层参数梯度的幅值还是较高的，但随着训练周期的增加，参数梯度的稀疏度显著增大，并且梯度稀疏度趋于稳定和饱和。在分布式SGD算法中，将这些0值附近的梯度进行交换，对网络带宽资源是一种极大的浪费，也就是说绝大多数（约99.9%）梯度交换都是冗余的。

梯度稀疏的目的在于压缩分布式训练时被传输的梯度数据，减少通信资源开销。由于SGD算法产生的梯度数值是高度噪声的，移除其中并不重要的部分并不会显著影响网络收敛过程，与之相反，有时还会带来正则化的效果，从而提升网络精度。

小结与讨论

相较于非结构化剪枝及启发式方法，结构化剪枝及自动化剪枝更易获得实际的模型加速机会及更高的模型压缩率。

卷积层相比全连接层的冗余性更小，更难以剪枝。

神经元剪枝相比权重剪枝更易损失模型精度。

训练阶段的梯度拥有最高的稀疏度。

对于随机初始化网络先进行剪枝再进行训练，有可能会比剪枝预训练网络获得更高的稀疏度和精度。因此，究竟剪枝后的残余连接结构与残余权重值两者哪个更为关键，就成为一个开放的研究问题。

11.3 模型压缩与硬件加速

模型压缩的一个潜在缺点是，部分经过压缩后的模型并不一定适用于传统的通用硬件，如CPU和GPU，往往需要定制化硬件的支持。 例如对于模型稀疏化后的网络模型来说，如果没有专用的稀疏计算库或者针对稀疏计算的加速器设计，则无法完全发挥稀疏所能带来的理论加速比。 对于经过数值量化之后的网络模型，很多硬件结构并不支持低比特运算，例如CPU 中只支持Short，Int，Float，Double等类型，而定制化硬件可以对不同比特的网络进行特定的支持。 因此，相关的研究工作如稀疏神经网络加速器和低比特神经网络加速器也被相继提出。

11.3.1 深度学习专用硬件

基于ASIC（Application Specific Integrated Circuit）实现AI专用芯片，可以在芯片电路级别对深度学习模型的计算和访存特性进行全面深度定制，相比于GPU可以达到更高的性能和效能提升。 当然AI专用芯片也损失了一定的通用性和灵活性。

得益于TPU在芯片内部定制了专用于矩阵乘法计算的脉动阵列架构，因此实现了比同时期CPU和GPU更高的计算效率。使得深度学习计算达到更高的吞吐量、更低的延迟和更高的能效。

11.3.2 稀疏模型硬件加速

结构化稀疏与非结构化稀疏

细粒度权值剪枝带来的的稀疏性，从计算来看非常的“不规则”，这对计算设备中的数据访存和大规模并行计算非常不友好。例如对GPU来说，使用cuSPARSE稀疏矩阵计算库来进行实验时，90%稀疏性（甚至更高）的矩阵的运算时间和一个完全稠密的矩阵运算时间相仿。这种“不规则”的稀疏通常被称为非结构化稀疏（Unstructured Sparsity）、细粒度稀疏（Fine-grained Sparsity）或随机稀疏（Random Sparsity）。

许多研究开始探索通过给神经网络剪枝添加一个“规则”的约束，使得剪枝后的稀疏模式更加适合硬件计算。 例如使非零值的位置分布不再是随机的，而是集中在规则的子结构中。 相比较于细粒度剪枝方法针对每个权值进行剪枝，粗粒度剪枝方法以组为单位对权值矩阵进行剪枝，使用组内的最大值或平均值为代表一组权值的重要性。 这种引入了“规则”的结构化约束的稀疏模式通常被称为结构化稀疏（Structured Sparsity）、粗粒度稀疏（Coarse-grained Sparsity）或块稀疏（Block Sparsity）。 但这种方法通常会牺牲模型的准确率和压缩比，结构化稀疏对非零权值的位置进行了限制，在剪枝过程中会将一些数值较大的权值剪枝，从而影响模型准确率。

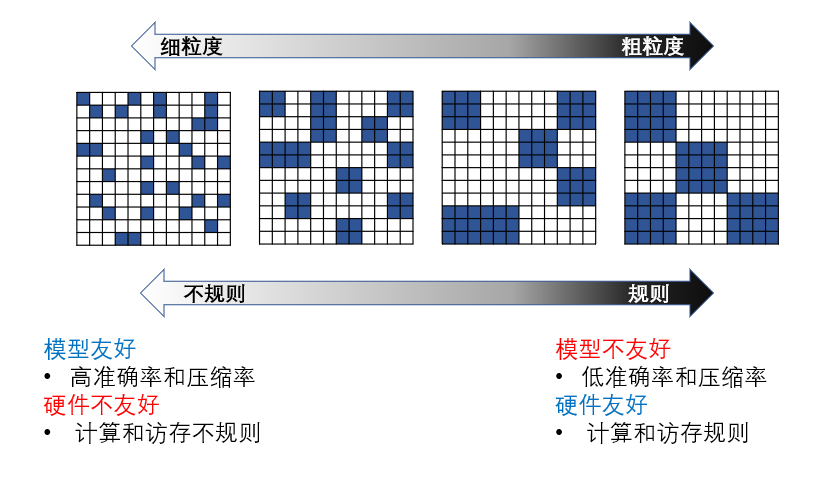
半结构化稀疏

权值稀疏的“随机”与计算的“规则”并非绝对矛盾，组平衡稀疏（Bank Balanced Sparsity）是在一种权值稀疏“随机”但非常适合硬件计算的稀疏化方法。在组平衡稀疏矩阵中，矩阵的每一行被分成了多个大小相等的组，每组中都有相同的稀疏度，即相同数目的非零值。

在下图的例子中，三个具有不同的稀疏结构的稀疏矩阵都是从图a中稠密权值矩阵剪枝得到的，稀疏度都是50%。细粒度剪枝会剪枝掉绝对值最小的50%的权值，从而得到了图 b 中的非结构化稀疏矩阵。粗粒度剪枝针对 2x2 的权值块进行剪枝，每块权值的重要性由块平均值代表，从而得到了图 c 中的结构化稀疏（块稀疏）矩阵。组平衡剪枝将每一个矩阵行分成了两个组（bank），每个组内进行独立的细粒度剪枝，去除在每个组内绝对值最小的 50% 的权值，从而得到了d图中的组平衡稀疏矩阵。

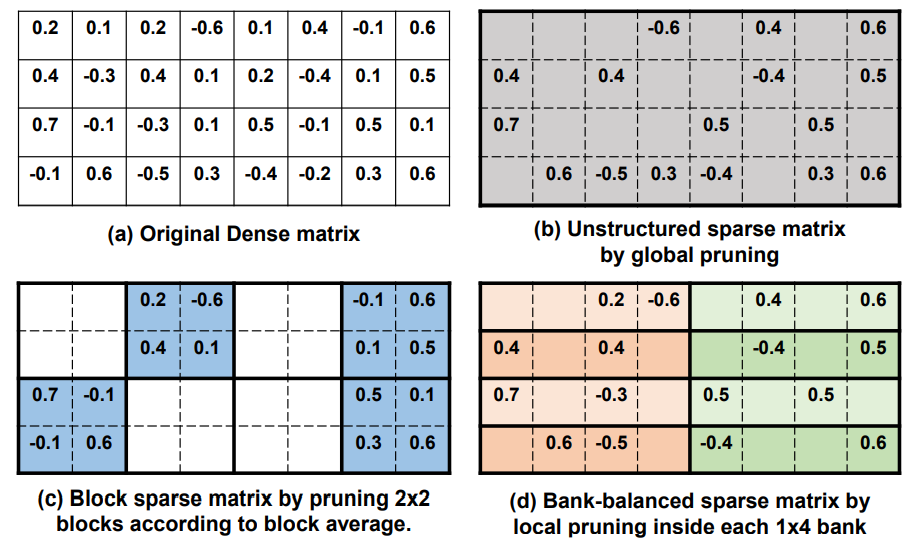
由于在每个bank内使用细粒度剪枝，因此能够很大程度地保留那些数值较大的权值，保持权值位置的随机分布，从而保持较高的模型准确率。同时这种方法得到的稀疏矩阵模式将矩阵进行了平衡的分割，这有利于硬件解决不规则的内存访问，并对矩阵运算实现高并行度。

英伟达在2020年发布了A100 GPU，其稀疏张量核使用了一种称为细粒度结构化稀疏（Fine-grained Structured Sparsity）的权值稀疏模式。 英伟达提出的细粒度结构化稀疏与组平衡稀疏解决的是相同的模型有效性和计算高效性的权衡问题，采用了相似的设计思想，因此稀疏结构也非常相似。细粒度结构化稀疏也称之为 2:4 结构化稀疏（2:4 Structured Sparsity）。在其剪枝过程中，权值矩阵首先被切分成大小固定为 4 的向量，并且稀疏度固定为50%（2:4）。2:4 结构化稀疏可以视为组平衡稀疏的一种特殊情况，即将组大小设置为4，将稀疏度设置为 50%。

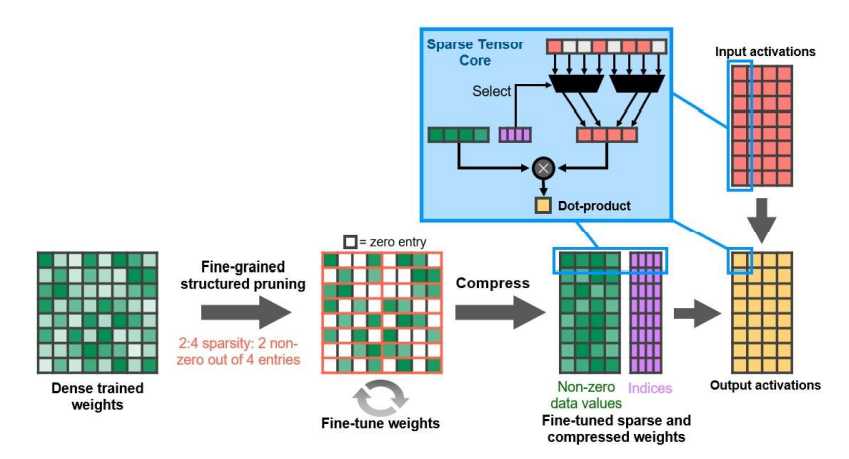
无论是组平衡稀疏，还是A100中提出的细粒度结构化稀疏，我们都可以将其称之为半结构化稀疏（Semi-structured Sparsity）。

11.3.2 量化模型硬件加速

对于量化模型的硬件加速方法较为直接，实现相应比特数的计算单元即可。在处理器芯片中，低比特计算单元可使用更少的硬件资源在更低的延迟内得出计算结果，并且大大降低功耗。TPU的推理芯片中很早就使用了INT8，在后续的训练芯片中也采用了BF16。英伟达从A100中已经集成了支持INT4、INT8、BF16的混合精度计算核心，在新发布的H100中甚至支持了BF8。