引入
对于二元分类问题,一个基本的思想是在样本空间中找到一个超平面,将样本分为两类。对于任意给定的\(w\in\mathbb{R}^p,b\in\mathbb{R}\),空间\(\mathbb{R}^p\)中的超平面可以表示为
\[\{x\in\mathbb{R}^p:w^Tx+b=0\},\]我们将此超平面记作\((w,b)\)。
假设\(y\in\{-1,1\}\)中,如果超平面可以分离样本,那么
\[\begin{cases} w^Tx_i+b\geq 1, &\text{if }y_i=1, \\ w^Tx_i+b\leq-1, &\text{if }y_i=-1. \end{cases}\]将两个超平面表示为
\[\begin{aligned} & H_1 = \{x \in \mathbb{R}^p : w^Tx + b = 1\}, \\ & H_2 = \{x \in \mathbb{R}^p : w^Tx + b = -1\}. \end{aligned}\]\(H_1\)和\(H_2\)是平行的,因为\(H_1\cap H_2=\emptyset\)。我们希望这两个超平面将样本分开,并且超平面之间的间隔最大化。
\(H_1\)和\(H_2\)之间的间隔为\(\frac{2}{\|w\|}\)。证明:
我们首先证明,对于任意\(x_1\in\mathbb{R}^p\),样本空间中的点\(x_1\)与超平面\((w,b)\)之间的距离为 \(\frac{\mid w^Tx_1+b \mid}{\| w \|}\)。
对于超平面\((w,b)\)上的任意两点\(x_2,x_3\),\(x_2-x_3\)是超平面\((w,b)\)上的向量,则\(w^T(x_2-x_3)=0\),这意味着向量\(w\)垂直于\((w,b)\)。将\(x_0\)表示为\(x_1\)在\((w,b)\)上的投影点,\(x_1\)与\((w,b)\)之间的距离为\(\| x_1-x_0\|\),则向量\(x_1-x_0\)与\((w,b)\)垂直,那么我们可以将其表示为\(x_1-x_0=\| x_1-x_0\|\frac{w}{\|w\|}\)。因此距离\(\|x_1-x_0\| = \sqrt{(x_1 - x_0)^T(x_1-x_0)} = \sqrt{\|x_1-x_0\| \frac{w^T}{\|w\|} (x_1 - x_0)} = \sqrt{ \frac{\|x_1-x_0\|}{\|w\|} (w^Tx_1 - w^Tx_0)} = \sqrt{ \frac{\|x_1-x_0\|}{\|w\|} (w^Tx_1 + b)}\) \(\implies \|x_1-x_0\|=\frac{\mid w^Tx_1+b \mid}{\| w \|}\)。
现在我们假设\(x_1\)在超平面\(H_1\)上,那么\(x_1\)和\(H_2\)之间的距离是\(\frac{\mid w^Tx_1+b+1 \mid}{\| w \|}=\frac{2}{\| w \|}. \square\)
我们注意到,最大化\(\frac{2}{\| w \|}\)与最小化\(\frac{\|w\|}{2}\)等价。
那么,对于线性可分的数据,支持向量机最大化两个超平面\(H_1,H_2\)的间隔:
\[\begin{equation*} \begin{aligned} & \min_{w,b} \frac{\|w\|}{2}, \\ & \text{ subject to } y_i(w^Tx_i+b) \geq 1, \forall i=1,\cdots,n. \end{aligned} \end{equation*}\]样本点\(\{(x_i, y_i): y_i(w^Tx_i+b) = 1\}\)位于超平面\(H_1,H_2\)上,称为支持向量。
软边缘支持向量机
实际数据通常不是线性可分的。设
\[z_i=y_i(w^Tx_i+b)-1,\]那么错误分类的样本是\(\{(x_i,y_i):z_i<0\}\)。
我们可以用损失函数来衡量误分类的严重程度。如0/1损失:
\[\ell_{\text{0/1}}(z)=\mathbf{1}(z<0).\]然而,这种损失函数不是凸函数,也不是连续的,因此不适合数值优化。因此,我们可以使用一些凸的连续的损失函数,称为替代损失函数。以下是三种常用的替代损失函数:
\[\begin{aligned} &\text{合叶损失 Hinge loss:}&\ell_{\text{hinge}}(z)=\max(0,1-z);\\ &\text{指数损失 Expometal loss:}&\ell_{\text{exp}}(z)=e^{-z};\\ &\text{对数损失 Logistic loss:}&\ell_{\text{log}}(z)=\ln(1+e^{-z}). \end{aligned}\]以下是这四种损失函数的图形:
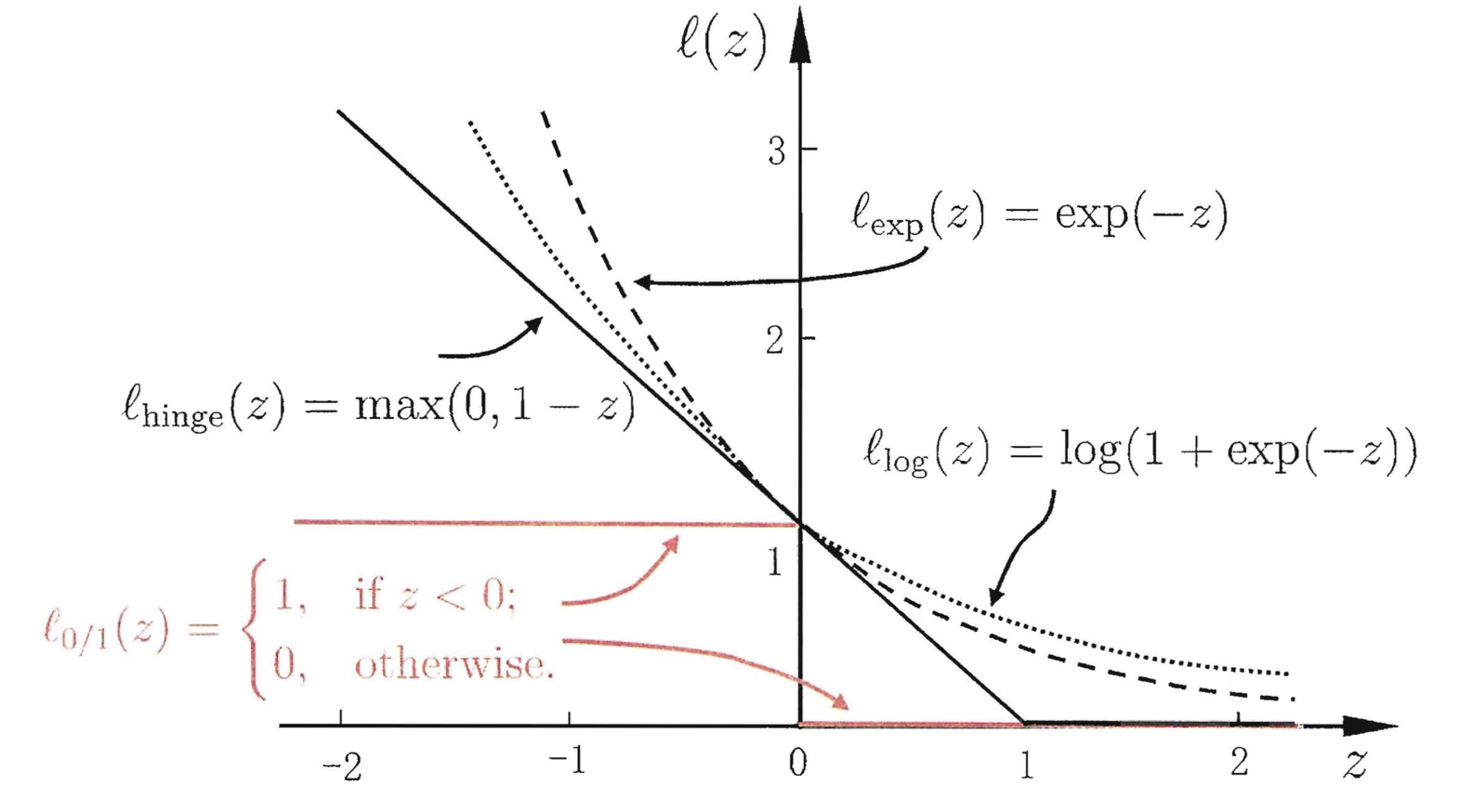
相较于其他两个替代损失函数,合叶损失对训练数据中的极端样本更鲁棒。本文以下内容我们使用合叶损失作为替代损失函数。
对每一个样本\((x_i,y_i)\),我们引入松弛变量\(\xi_i\)
\[\xi_i = \ell_{\text{hinge}}(z_i+1) = \max\left(0, 1 - y_i(w^Tx_i+b)\right).\]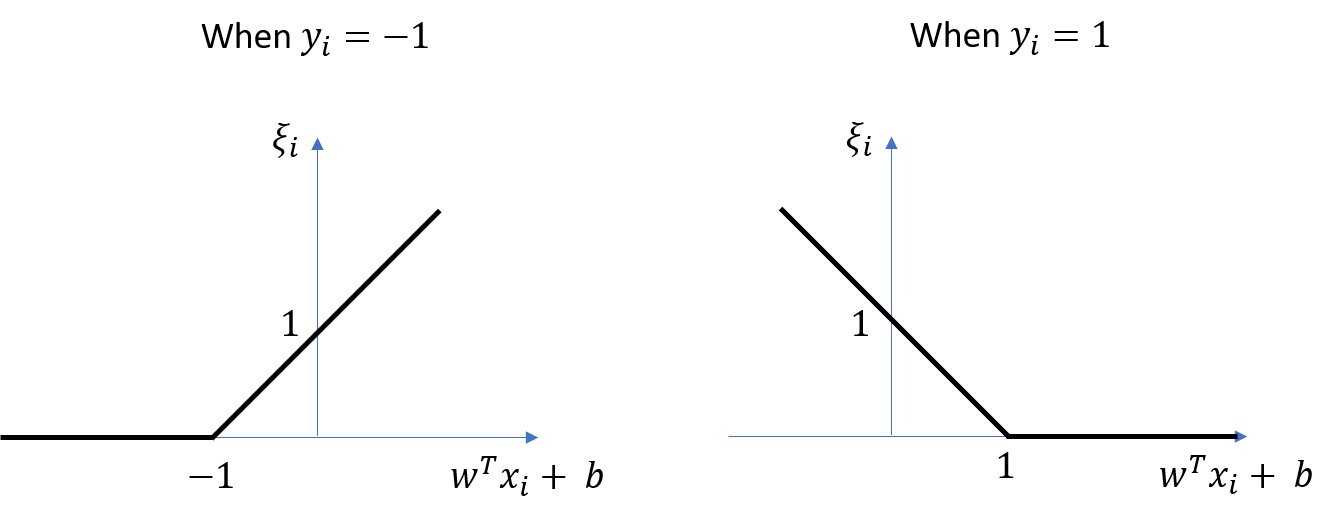
对于给定的超参数 \(C > 0\), 软间隔支持向量机的优化问题可表示为
\[\begin{equation*} \begin{aligned} & \min_{w,b} \frac{\|w\|}{2} + C \sum_{i=1}^{n} \xi_i,\\ & \text{ subject to } \begin{cases} y_i(w^Tx_i+b) \geq 1-\xi_i, \\ \xi_i\geq0, \end{cases} \ \ \forall i=1,\cdots,n. \end{aligned} \end{equation*}\]样本点\(\{(x_i, y_i): y_i(\hat{w}^Tx_i+\hat{b}) \leq 1\}\)是支持向量。
设\(\hat{w},\hat{b}\)为以上优化问题的最优解,那么分隔超平面为
\[\{x\in\mathbb{R}^p:\hat{w}^T x+\hat{b}=0\}\]分类决策函数为
\[\hat{y}=\text{sign}(\hat{w}^Tx+\hat{b})。\]对偶问题
对偶优化问题
软间隔支持向量机的优化问题对应的拉格朗日函数为 \(\mathcal{L}(w,b,\xi,\alpha,\mu) = \frac{\|w\|^2}{2} + C \sum_{i=1}^{n} \xi_i + \sum_{i=1}^n \alpha_i [1 - \xi_i - y_i(w^Tx_i + b)] - \sum_{i=1}^n\mu_i\xi_i,\) 其中\(\alpha_i \geq 0, \mu_i \geq 0\)是拉格朗日乘子。
设 \(\mathcal{D}(\alpha,\mu) = \min_{w,b,\xi} \mathcal{L}(w,b,\xi,\alpha,\mu).\) 则软间隔支持向量机的优化问题对应的对偶优化问题为
\[\max_{\alpha, \mu: \alpha_i \geq 0, \mu_i \geq 0} \mathcal{D}(\alpha,\mu) = \max_{\alpha, \mu: \alpha_i \geq 0, \mu_i \geq 0} \min_{w,b,\xi} \mathcal{L}(w,b,\xi,\alpha,\mu).\]将函数\(\mathcal{L}(w,b,\xi,\alpha,\mu)\)分别对\(w,b,\xi_i\)求导,然后设为\(0\), 得到
\[\begin{aligned} & \frac{\partial \mathcal{L}(w,b,\xi,\alpha,\mu)}{\partial w} = w - \sum_{i=1}^{n} \alpha_i y_i x_i = 0 \implies w = \sum_{i=1}^{n} \alpha_i y_i x_i, \\ & \frac{\partial \mathcal{L}(w,b,\xi,\alpha,\mu)}{\partial b} = - \sum_{i=1}^{n} \alpha_i y_i = 0 \implies \sum_{i=1}^{n} \alpha_i y_i = 0, \\ & \frac{\partial \mathcal{L}(w,b,\xi,\alpha,\mu)}{\partial \xi_i} = C - \alpha_i - \mu_i = 0 \implies \alpha_i + \mu_i = C. \end{aligned}\]代入回函数\(\mathcal{L}(w,b,\xi,\alpha,\mu)\),则对偶优化问题可表示为
\[\begin{equation*} \begin{aligned} & \max_{\alpha} \mathcal{D}(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{i'=1}^n \alpha_i\alpha_{i'}y_iy_{i'}x_i^Tx_{i'}, \\ & \text{ subject to } \begin{cases} \sum_{i=1}^n \alpha_iy_i=0, \\ 0\leq\alpha_i\leq C , \end{cases} \ \ \forall i=1,\cdots,n. \end{aligned} \end{equation*}\]KKT条件为
\[\begin{cases} \alpha_i \geq 0, \\ \mu_i \geq 0, \\ y_i(w^Tx_i+b) - 1 + \xi_i \geq 0, \\ \alpha_i[y_i(w^Tx_i+b) - 1 + \xi_i] = 0, \\ \xi_i \geq 0, \\ \mu_i\xi_i = 0. \end{cases}\]转换成对偶问题后,约束条件被简化了,并且可以使用核技巧。
SMO算法
我们用SMO(序列最小最优化,sequential minimal optimization)算法来解该对偶优化问题。其基本思路是:如果所有变量的解满足KKT条件,那么这些变量就是最优化问题的解,因为KKT条件是该最优化问题的充分必要条件。
迭代以下两步直至收敛 {
- 找到一个违反KKT条件最严重的\(α_i\),然后找到使得\(w^Tx_{i'}+b\)与真实值\(y_{i'}\)相差最大的\(i'\)对应的\(α_{i'}\),这里的\(w=\sum_{l=1}^n \alpha_{l} y_{l}x_{l}\).
- 维持其他的\(α_{i''}\)不变,在对偶优化问题的约束条件下求解二次规划问题:\(\max_{\alpha_i,\alpha_{i'}}\mathcal{D}(\alpha)\). }
该对偶优化问题的解为
\[\hat{\alpha} = (\hat{\alpha}_1, \hat{\alpha}_2, \cdots, \hat{\alpha}_n) = \arg\max_{\alpha} \mathcal{D}(\alpha),\]SMO算法的详细介绍可参见李航的《统计学习方法》7.4 序列最小优化算法。
原问题的解
在求得解\(\hat{\alpha}\)后, 可计算
\[\hat{w} = \sum_{i=1}^n \hat{\alpha}_{i} y_{i}x_{i}.\]下标在以下集合\(I^*\)中的样本点\((x_i,y_i)\)是支持向量:
\[I^* = \{ i^*: \hat{\alpha}_{i^*} \neq 0 \} = \{ i^*: 0 < \hat{\alpha}_{i^*} \leq C \}.\]然后我们可通过任一支持向量\((x_{i^*},y_{i^*})\)来计算截距项\(\hat{b}\):
\[\hat{b} = y_{i^*} - \hat{w}^Tx_{i^*} = y_{i^*} - \sum_{i=1}^n \hat{\alpha}_{i} y_{i}x_{i}^T x_{i^*}.\]在实践中,出于鲁棒性的考虑,我们通常采用所有(或部分)支持向量计算的\(\hat{b}\)的平均值:
\[\hat{b} = \frac{1}{\mid I^* \mid} \sum_{i^* \in I^*} \left( y_{i^*} - \hat{w}^Tx_{i^*} \right) = \frac{1}{\mid I^* \mid} \sum_{i^* \in I^*} \left( y_{i^*} - \sum_{i=1}^n \hat{\alpha}_{i} y_{i}x_{i}^T x_{i^*} \right).\]在得到\(\hat{w}\)和\(\hat{b}\)后,分隔超平面为
\[\left\{ x\in\mathbb{R}^p: \hat{w}^T{x} + \hat{b} = 0 \right\} = \left\{ x\in\mathbb{R}^p: \sum_{i=1}^n \hat{\alpha}_{i} y_{i}x_{i}^T x + \frac{1}{\mid I^* \mid} \sum_{i^* \in I^*} \left( y_{i^*} - \sum_{i=1}^n \hat{\alpha}_{i} y_{i}x_{i}^T x_{i^*} \right) = 0 \right\}.\]分类决策函数为
\[\hat{y} = \text{sign} \left( \hat{w}^Tx + \hat{b} \right).\]支持向量
对于任一样本\((x_i,y_i)\), 有以下五种可能的情形。
若\(\alpha_i=0\), 则\(\mu_i=C,\xi_i=0\)。该样本(如下图中的\(x_1\))不影响超平面\(\left\{ x\in\mathbb{R}^p: \hat{w}^T{x} + \hat{b} = 0 \right\}\)的估计,该样本也不是支持向量。
否则,若\(0 < \alpha_i \leq C\),则该样本为支持向量。
若\(0<\alpha_i<C\),则\(\mu_i=C-\alpha_i,\xi_i=0\)。该样本(如下图中的\(x_2\))被正确分类,且该样本在超平面\(H_1\)(若\(y_i=1\))或\(H_2\)(若\(y_i=-1\))上。
若\(\alpha_i=C\),则\(\mu_i=0\),而\(\frac{\xi_i}{\|w\|}\)为样本至超平面\(H_1\)(若\(y_i=1\))或\(H_2\)(若\(y_i=-1\))的距离。
若\(\alpha_i=C\)且\(0<\xi_i<1\),则\(\mu_i=0\)。该样本(如下图中的\(x_3\))被正确分类。
若\(\alpha_i=C\)且\(\xi_i=1\),则\(\mu_i=0\)。该样本(如下图中的\(x_4\))在分隔平面上。
若\(\alpha_i=C\)且 \(\xi_i>1\),则\(\mu_i=0\)。该样本(如下图中的\(x_5,x_6\))被误分类。
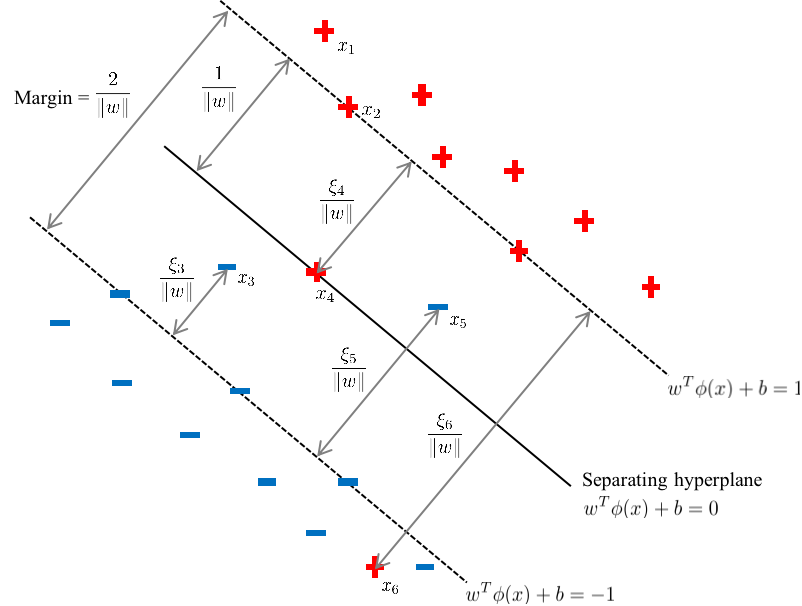
这五种情形总结为表格
| \(\alpha_i\) | \(\mu_i\) | \(\xi_i\) | 是否正确分类? | 是否为支持向量? | 是否在超平面上? |
|---|---|---|---|---|---|
| \(0\) | \(C\) | \(0\) | 是 | 否 | 否 |
| \(0<\alpha_i<C\) | \(C-\alpha_i\) | \(0\) | 是 | 是 | 在超平面\(H_1\)(若\(y_i=1\))或\(H_2\)(若\(y_i=-1\))上 |
| \(C\) | \(0\) | \(0<\xi_i<1\) | 是 | 是 | 否 |
| \(C\) | \(0\) | \(1\) | / | 是 | 在分隔平面上 |
| \(C\) | \(0\) | \(\xi_i>1\) | 否 | 是 | 若\(\xi_i=2\),在超平面\(H_2\)(若\(y_i=1\))或\(H_1\)(若\(y_i=-1\))上;否则不在超平面上 |
核SVM
映射到高维空间
如果原数据线性不可分,映射到高维空间后可以使之线性可分。
下图中,左边的数据点在原始特征空间中是线性不可分的,但在右边的更高维的特征空间中是线性可分的。
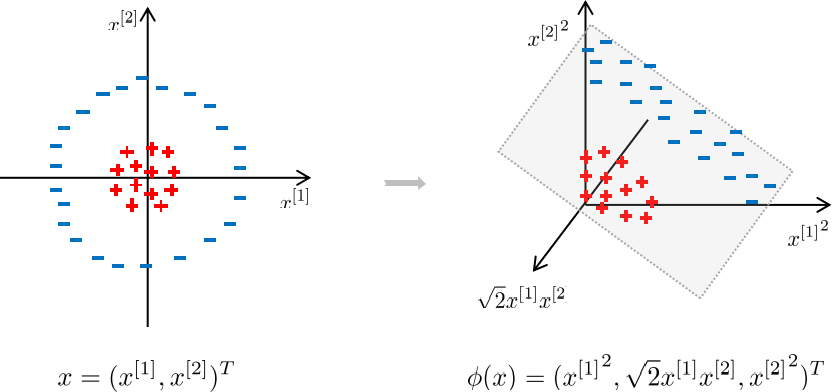
设\(\phi:\mathbb{R}^p \to \mathbb{R}^\tilde{p}\)为低维到高维的映射函数,\(\phi(x)\)为将原特征向量\(x\)映射到高维空间之后的高维特征向量。 \(x \in \mathbb{R}^p \to \phi(x) \in \mathbb{R}^\tilde{p}.\)
在高维空间中的两个超平面为
\[\{x \in \mathbb{R}^p : w^T \phi(x) + b = \pm 1\}.\]软间隔支持向量机的优化问题可表示为
\[\begin{equation*} \begin{aligned} & \min_{w,b} \frac{\|w\|}{2} + C \sum_{i=1}^{n} \xi_i, \\ & \text{ subject to } \begin{cases} y_i(w^T \phi(x_i)+b) \geq 1-\xi_i, \\ \xi_i \geq 0, \end{cases} \ \ \forall i=1,\cdots,n. \end{aligned} \end{equation*}\]转化成对偶问题
\[\begin{equation*}\begin{aligned}& \min_{\alpha} \mathcal{D}(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{i'=1}^n \alpha_i\alpha_{i'}y_iy_{i'} \phi(x_i)^T \phi(x_{i'}), \\ & \text{ subject to } \begin{cases} \sum_{i=1}^n \alpha_iy_i=0, \\ 0\leq\alpha_i\leq C , \end{cases} \ \ \forall i=1,\cdots,n. \end{aligned} \end{equation*}\]核技巧
向量\(\phi(x)\) 通常有较高的维度 \(\tilde{p}\), 计算点积 \(\phi(x_i)^T \phi(x_{i'})\) 的复杂度 \(O(\tilde{p})\) 通常较大. 为处理这一问题,我们采用核技巧。
核函数定义为
\[\mathcal{K}(x_i, x_{i'}) = \phi(x_i)^T \phi(x_{i'}).\]我们可以使用核函数在原始特征空间\(\mathbb{R}^p\)中计算\(\mathcal{K}(x_i, x_{i'})\)来得到高维特征空间\(\mathbb{R}^\tilde{p}\)中的点积\(\phi(x_i)^T \phi(x_{i'})\),而计算\(\mathcal{K}(x_i, x_{i'})\)的复杂度为\(O(p)\),这远小于直接计算 \(\phi(x_i)^T \phi(x_{i'})\) 的复杂度 \(O(\tilde{p})\)。
使用核技巧之后,对偶问题转化为
\[\begin{equation*}\begin{aligned}& \min_{\alpha} \mathcal{D}(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{i'=1}^n \alpha_i\alpha_{i'}y_iy_{i'} \mathcal{K}(x_i, x_{i'}), \\ & \text{ subject to } \begin{cases} \sum_{i=1}^n \alpha_iy_i=0, \\ 0\leq\alpha_i\leq C , \end{cases} \ \ \forall i=1,\cdots,n. \end{aligned} \end{equation*}\]分隔超平面转化为
\[\left\{ x\in\mathbb{R}^p: \hat{w}^T{x} + \hat{b} = 0 \right\} = \left\{ x\in\mathbb{R}^p: \sum_{i=1}^n \hat{\alpha}_{i} y_{i}\mathcal{K}(x_i, x) + \frac{1}{\mid I^* \mid} \sum_{i^* \in I^*} \left( y_{i^*} - \sum_{i=1}^n \hat{\alpha}_{i} y_{i}\mathcal{K}(x_i, x_{i^*}) \right) = 0 \right\}.\]另外,核矩阵定义为
\[\mathbf{K} = \begin{pmatrix} \mathcal{K}(x_1, x_1) & \mathcal{K}(x_1, x_2) & \cdots & \mathcal{K}(x_1, x_{n}) \\ \mathcal{K}(x_2, x_1) & \mathcal{K}(x_2, x_2) & \cdots & \mathcal{K}(x_2, x_{n}) \\ \vdots & \vdots & \ddots & \vdots \\ \mathcal{K}(x_n, x_1) & \mathcal{K}(x_n, x_2) & \cdots & \mathcal{K}(x_n, x_{n}) \end{pmatrix}.\]核矩阵是半正定的。其实,一个函数可以用作核函数的充分必要条件是,该函数是对称的且对应的核矩阵是半正定的。该函数是对称的是指对任意 \(i,i'\)都有\(\mathcal{K}(x_i, x_{i'}) = \mathcal{K}(x_{i'}, x_i)\)。
一些常用的核函数:
| 核函数名称 | 表达式 | 参数 |
|---|---|---|
| 线性 Linear | \(\mathcal{K}(x_i, x_{i'})=x_i^Tx_{i'}\) | |
| 多项式 Polynomial | \(\mathcal{K}(x_i, x_{i'})=(x_i^Tx_{i'})^d\) | 多项式次数 \(d > 1\) |
| RBF (or 高斯 Gaussian) | \(\mathcal{K}(x_i, x_{i'})=\exp (-| x_i - x_{i'} |/2\sigma^2)\) | 宽度 \(\sigma>0\) |
| 拉普拉斯 Laplace | \(\mathcal{K}(x_i, x_{i'})=\exp (-| x_i - x_{i'}|/\sigma)\) | \(\sigma>0\) |
| Sigmoid | \(\mathcal{K}(x_i, x_{i'})=\text{tanh}(\beta x_i^Tx_{i'} + \theta)\) | \(\beta>0, \theta<0\) |
选择核函数的经验准则:
- 如果原数据样本量不大,且特征维度高,通常这样的数据是线性(近似)可分的,可采用线性核函数;
- 如果原数据样本量较大,且特征维度不高,通常使用高斯核函数。
我们注意到,支持向量机若使用线性核函数则为线性分类器,否则为非线性核函数。
其他
支持向量机的优化问题是凸优化,因此其解一定是全剧最优解。
由于支持向量机的构建只依赖于支持向量,相较于其他算法, 支持向量机更适合小样本高维数据的的建模。
支持向量机的构建对样本不均衡问题不太敏感,因为其优化目标极小化超平面间隔和支持向量带来的松弛变量。所以只要支持向量相对均衡,支持向量机受样本不均衡问题的影响就不会太大。
参考资料:
Lecture notes from my professor Min Xu.
周志华. 第6章 支持向量机. 机器学习. 清华大学出版社, 2016.
李航. 第7章 支持向量机. 统计学习方法. 清华大学出版社, 2012.
张皓. 从零推导支持向量机(SVM).
