Feature Scaling and Zero-Centering

Why Feature Scaling

Since the range of values of different features varies widely, in some machine learning algorithms, objective functions will not work properly. Feature scaling makes the values of different features approximately in the same scale.

There are several reasons why we need feature scaling.

Firstly, many algorithms (such as K-means, KNN) calculate the distance between two points by the Euclidean distance. If one of the features has a broad range of values, the distance will be governed by this particular feature.

Secondly, L1 or L2 regularization penalize the weights. If a feature has a small scale, the weight corresponding to this feature tends to be large, and the penalization for the weight of this feature will be heavier and that is unfair.

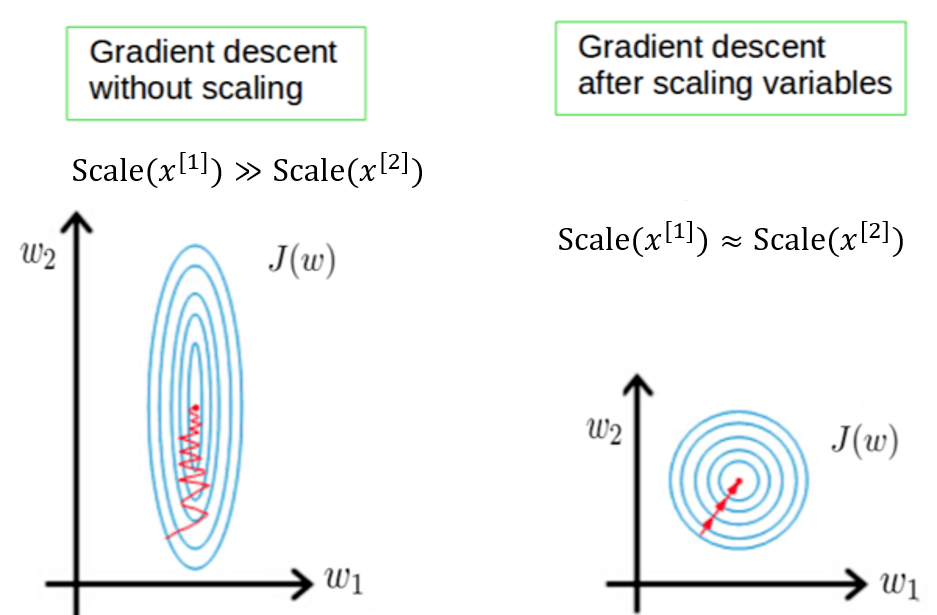
Thirdly, feature scaling helps gradient descent converges faster. Suppose the scale of feature \(x^{[1]}\) is large and that of \(x^{[2]}\) is small, that leads to the range of weight \(w_1\) is smaller than the range of \(w_2\). The problem is that these gradients usually share the same learning rate. If the learning rate is large, then \(w_1\) cannot converge. Otherwise, if the learning rate is small, then \(w_2\) converges very slow.

Why Zero-Centering

We also expect the features are zero-centered, otherwise it could introduce undesirable zig-zagging dynamics in the gradient updates for the weights.

Say a model has inputs \(x = (x^{[1]}, x^{[2]}, \cdots)^T\), weights \(w=(w_1,w_2,\cdots)^T\), and output \(\hat{y}=\sigma(w^Tx+b)\). Denote a intermediate variable \(z:=w^Tx+b\). The gradients of the weight \(w_j\) is

\[\frac{\partial \text{Loss}}{\partial w_j} = \frac{\partial \text{Loss}}{\partial z} \frac{\partial z}{\partial w_j} = \frac{\partial \text{Loss}}{\partial z} x^{[j]}.\]

If all \(x^{[j]}>0\) or \(<0\) for \(j=1,2,\cdots\), the gradients \(\frac{\partial \text{Loss}}{\partial w_j}\) for all $j$ have the same sign (positive or negative) as \(\frac{\partial \text{Loss}}{\partial z}\).

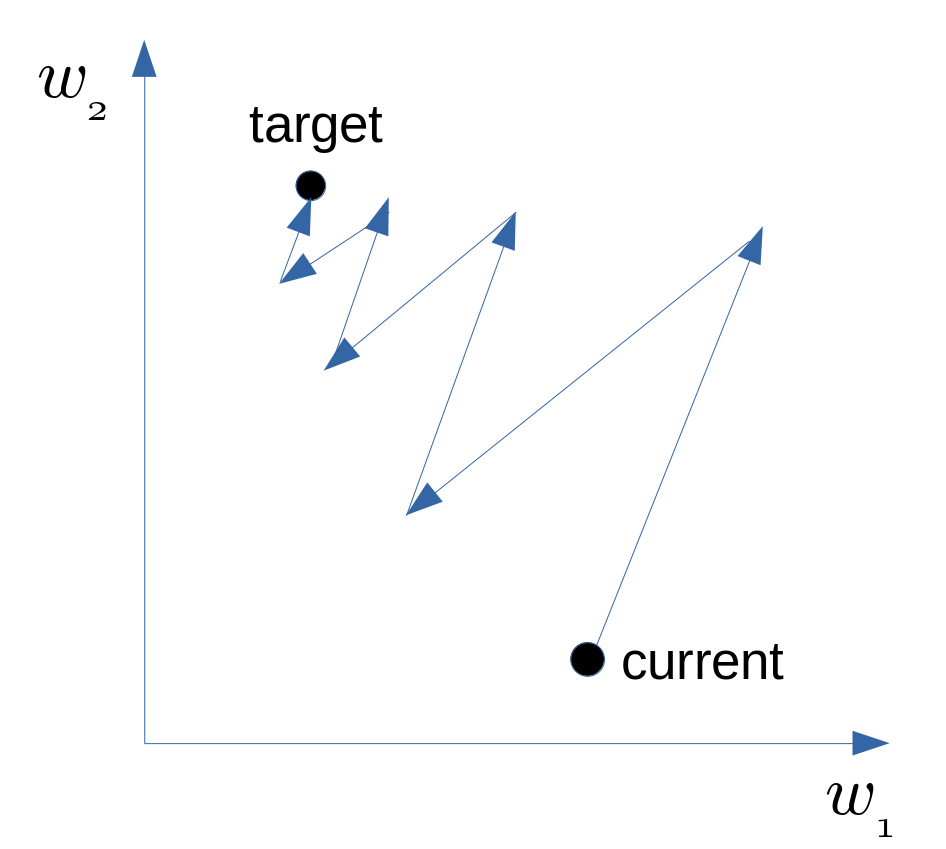
Now let’s show why the same sign of gradients may leads to zig-zagging. Say there are two parameters \(w_1,w_2\), and the gradients of them are always of the same sign. That means \(w_1\) and \(w_2\) increase or decrease simultaneously in the gradient updates, and it also means that we can only move roughly in the direction of northeast or southwest in the parameter space. If our goal happens to be in the northwest or southeast side of our current position, then it will cost a lot to move to our target position, as shown below.

Common Methods

Standardization:

\[x^* = \frac{x-\bar{x}}{\text{std}(x)}.\]

Mean normalization:

\[x^* = \frac{x-\bar{x}}{\text{max}(x) - \text{min}(x)}.\]

Reference:

Wikipedia: Feature scaling.